Observables

Radial Distribution Functions

Module: RDF

class pytim.observables.rdf.RDF(universe, max_distance='full', nbins=75, start=None, stop=None, step=None, observable=None, observable2=None, **kargs)[source]

Calculates a radial distribution function of some observable from two groups.

The two functions must return an array (of scalars or of vectors) having the same size of the group. The scalar product between the two functions is used to weight the distriution function.

g(r) = \frac{1}{N}\left\langle \sum_{i\neq j} \delta(r-|r_i-r_j|)\ f_1(r_i,v_i)\cdot f_2(r_j,v_j) \right\rangle

Parameters:

  • max_radius (double) – compute the rdf up to this distance. If ‘full’ is supplied (default) computes it up to half of the smallest box side.

  • nbins (int) – number of bins

  • observable (Observable) – observable for the first group

  • observable2 (Observable) – observable for the second group

Example:

>>> import MDAnalysis as mda
>>> import numpy as np
>>> import pytim
>>> from pytim import observables
>>> from pytim.datafiles import *
>>>
>>> u = mda.Universe(WATER_GRO,WATER_XTC)
>>> oxygens = u.select_atoms("name OW")
>>>
>>> nres = observables.NumberOfResidues()
>>>
>>> rdf = observables.RDF(u,nbins=120,observable=nres,observable2=nres)
>>>
>>> interface = pytim.ITIM(u,alpha=2.,group=oxygens,cluster_cut=3.5,molecular=False)
>>>
>>> for ts in u.trajectory[::50]:
...     layer=interface.layers[0,0]
...     rdf.sample(layer,layer)
>>> rdf.count[0]=0
>>> np.savetxt('RDF3D.dat', np.column_stack((rdf.bins,rdf.rdf)))

Note that one needs to specify neither both groups, not both observables. If only the first group (observable) is specified, the second is assumed to be the same as the first, as in the following example:

>>> rdf1 = observables.RDF(u,observable=nres)
>>> rdf2 = observables.RDF(u,observable=nres)
>>> rdf3 = observables.RDF(u,observable=nres,observable2=nres)
>>>
>>> rdf1.sample(layer)
>>> rdf2.sample(layer,layer)
>>> rdf3.sample(layer,layer)
>>> print (np.all(rdf1.rdf[:]==rdf2.rdf[:]))
True
>>> print (np.all(rdf1.rdf[:]==rdf3.rdf[:]))
True
class pytim.observables.rdf.oldRDF(universe, nbins=75, max_radius='full', start=None, stop=None, step=None, observable=None, observable2=None, kargs1=None, kargs2=None)[source]

Calculates a radial distribution function of some observable from two groups.

The two functions must return an array (of scalars or of vectors) having the same size of the group. The scalar product between the two functions is used to weight the distriution function.

g(r) = \frac{1}{N}\left\langle \sum_{i\neq j} \delta(r-|r_i-r_j|)\ f_1(r_i,v_i)\cdot f_2(r_j,v_j) \right\rangle

Parameters:

  • max_radius (double) – compute the rdf up to this distance. If ‘full’ is supplied (default) computes it up to half of the smallest box side.

  • nbins (int) – number of bins

  • observable (Observable) – observable for the first group

  • observable2 (Observable) – observable for the second group

Example:

>>> import MDAnalysis as mda
>>> import numpy as np
>>> import pytim
>>> from pytim import observables
>>> from pytim.datafiles import *
>>>
>>> u = mda.Universe(WATER_GRO,WATER_XTC)
>>> oxygens = u.select_atoms("name OW")
>>>
>>> nres = observables.NumberOfResidues()
>>>
>>> rdf = observables.RDF(u,nbins=120,observable=nres,observable2=nres)
>>>
>>> interface = pytim.ITIM(u,alpha=2.,group=oxygens,cluster_cut=3.5,molecular=False)
>>>
>>> for ts in u.trajectory[::50]:
...     layer=interface.layers[0,0]
...     rdf.sample(layer,layer)
>>> rdf.count[0]=0
>>> np.savetxt('RDF3D.dat', np.column_stack((rdf.bins,rdf.rdf)))

Note that one needs to specify neither both groups, not both observables. If only the first group (observable) is specified, the second is assumed to be the same as the first, as in the following example:

>>> rdf1 = observables.RDF(u,observable=nres)
>>> rdf2 = observables.RDF(u,observable=nres)
>>> rdf3 = observables.RDF(u,observable=nres,observable2=nres)
>>>
>>> rdf1.sample(layer)
>>> rdf2.sample(layer,layer)
>>> rdf3.sample(layer,layer)
>>> print (np.all(rdf1.rdf[:]==rdf2.rdf[:]))
True
>>> print (np.all(rdf1.rdf[:]==rdf3.rdf[:]))
True

Module: RDF2D

class pytim.observables.rdf2d.RDF2D(universe, nbins=75, max_radius='full', start=None, stop=None, step=None, excluded_dir='auto', true2D=False, observable=None, kargs1=None, kargs2=None)[source]

Calculates a radial distribution function of some observable from two groups, projected on a plane.

The two functions must return an array (of scalars or of vectors) having the same size of the group. The scalar product between the two functions is used to weight the distriution function.

Parameters:

  • nbins (int) – number of bins

  • excluded_dir (char) – project position vectors onto the plane orthogonal to ‘z’,’y’ or ‘z’

  • observable (Observable) – observable for group 1

  • observable2 (Observable) – observable for group 2

Example:

>>> import MDAnalysis as mda
>>> import numpy as np
>>> import pytim
>>> from pytim import *
>>> from pytim.datafiles import *
>>>
>>> u = mda.Universe(WATER_GRO,WATER_XTC)
>>> oxygens = u.select_atoms("name OW")
>>> interface = pytim.ITIM(u,alpha=2.,group=oxygens,        cluster_cut=3.5,molecular=False)
>>> rdf = observables.RDF2D(u,nbins=250)
>>>
>>> for ts in u.trajectory[::50] :
...     layer=interface.layers[0,0]
...     rdf.sample(layer,layer)
>>> rdf.count[0]=0
>>> np.savetxt('RDF.dat', np.column_stack((rdf.bins,rdf.rdf)))

This results in the following RDF (sampling more frequently):

(Source code, png, hires.png, pdf)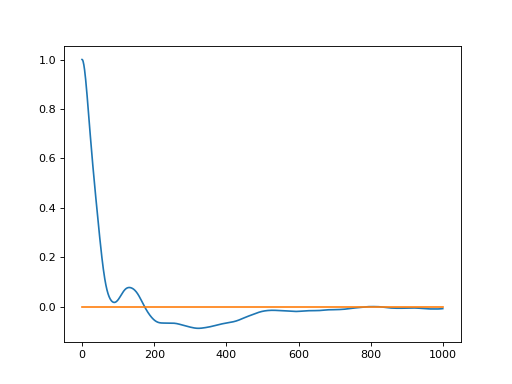

_images/observables-1.png

Profiles

Module: Profile

class pytim.observables.profile.Profile(direction=None, observable=None, interface=None, symmetry='default', mode='default', MCnorm=True, **kargs)[source]

Calculates the profile (normal, or intrinsic) of a given observable across the simulation box.

Parameters:

  • observable (Observable) – Number, Mass, or any other observable: calculate the profile of this quantity. If None is supplied, it defaults to the number density. The number density is always calculated on a per atom basis.

  • interface (ITIM) – if provided, calculate the intrinsic profile with respect to the first layers

  • direction (str) – ‘x’,’y’, or ‘z’ : calculate the profile along this direction. (default: ‘z’ or the normal direction of the interface, if provided.

  • MCnorm (bool) – if True (default) use a simple Monte Carlo estimate the effective volumes of the bins.

Keyword Arguments:

  • MCpoints (int) – number of points used for MC normalization (default, 10x the number of atoms in the universe)

Example (non-intrinsic, total profile + first 4 layers ):

>>> import numpy as np
>>> import MDAnalysis as mda
>>> import pytim
>>> from   pytim.datafiles import *
>>> from   pytim.observables import Profile
>>>
>>> u = mda.Universe(WATER_GRO,WATER_XTC)
>>> g = u.select_atoms('name OW')
>>> # here we calculate the profiles of oxygens only (note molecular=False)
>>> inter = pytim.ITIM(u,group=g,max_layers=4,centered=True, molecular=False)
>>>
>>> # We create a list of 5 profiles, one for the total and 4 for the first
>>> # 4 layers.
>>> # Note that by default Profile() uses the number of atoms as an observable
>>> Layers = []
>>> for n in range(5):
...     Layers.append(Profile())
>>>
>>> # Go through the trajectory, center the liquid slab and sample the profiles
>>> for ts in u.trajectory[::50]:
...         # this shifts the system so that the center of mass of the liquid slab
...         # is in the middle of the box
...         inter.center()
...
...         Layers[0].sample(g)
...         Layers[1].sample(u.atoms[u.atoms.layers == 1 ])
...         Layers[2].sample(u.atoms[u.atoms.layers == 2 ])
...         Layers[3].sample(u.atoms[u.atoms.layers == 3 ])
...         Layers[4].sample(u.atoms[u.atoms.layers == 4 ])
>>>
>>> density=[]
>>> for L in Layers:
...     low,up,avg = L.get_values(binwidth=0.5)
...     density.append(avg)
>>>
>>> # (low + up )/2 is the middle of the bin
>>> np.savetxt('profile.dat',list(zip(low,up,density[0],density[1],density[2],density[3],density[4])))

This results in the following profile (sampling more often and zooming close to the interface border)

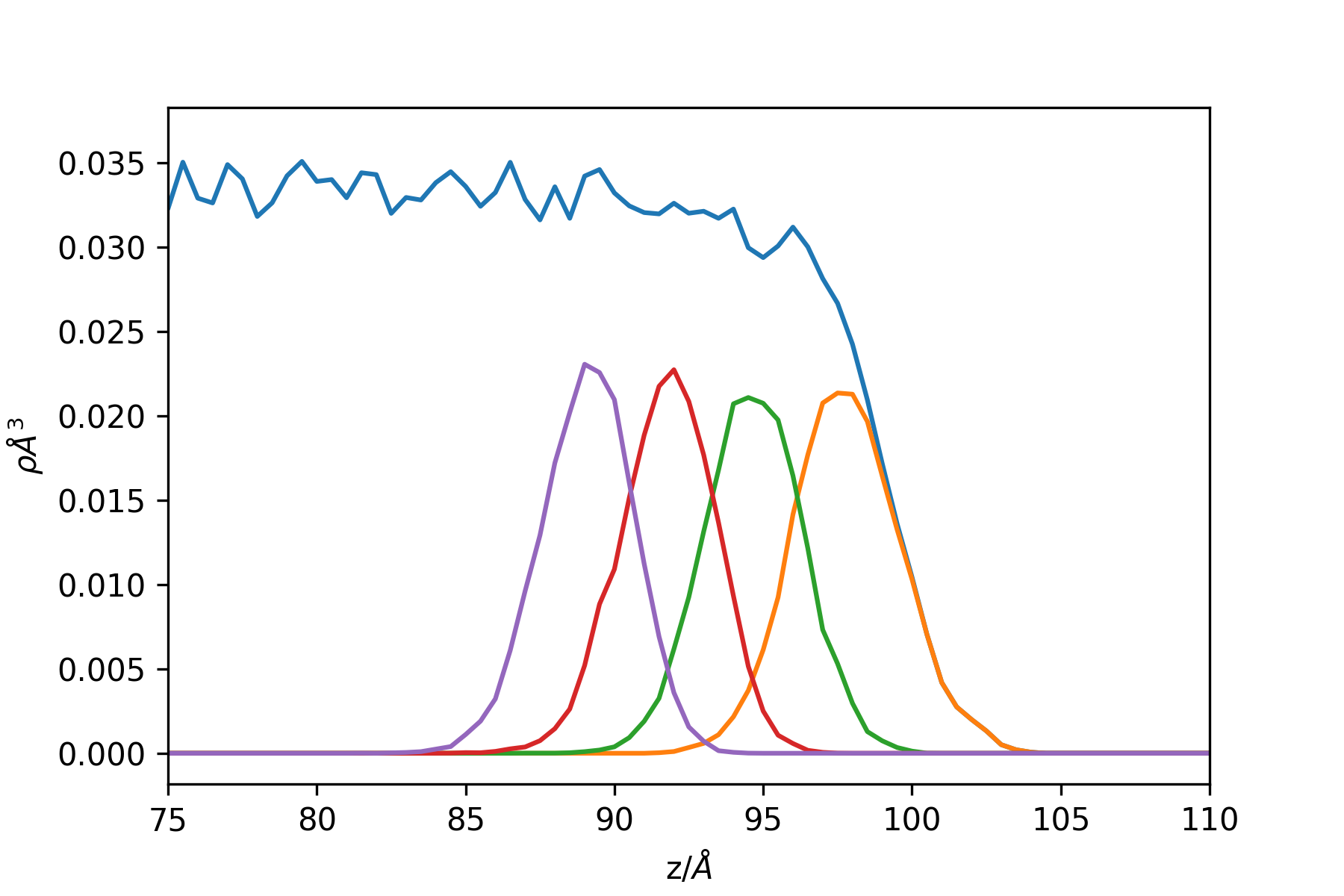
_images/nonintrinsic_water.png

Example: the intrinsic profile of a LJ liquid/vapour interface:

>>> import numpy as np
>>> import MDAnalysis as mda
>>> import pytim
>>> from   pytim.datafiles import LJ_GRO, LJ_SHORT_XTC
>>> from   pytim.observables import Profile

>>> u = mda.Universe(LJ_GRO,LJ_SHORT_XTC)
>>>
>>> inter = pytim.ITIM(u,alpha=2.5,cluster_cut=4.5)
>>> profile = Profile(interface=inter)
>>>
>>> for ts in u.trajectory:
...     profile.sample(u.atoms)
>>>
>>> low, up, avg = profile.get_values(binwidth=0.5)
>>> np.savetxt('profile.dat',list(zip(low,up,avg)))

This results in the following profile (sampling a longer trajectory):

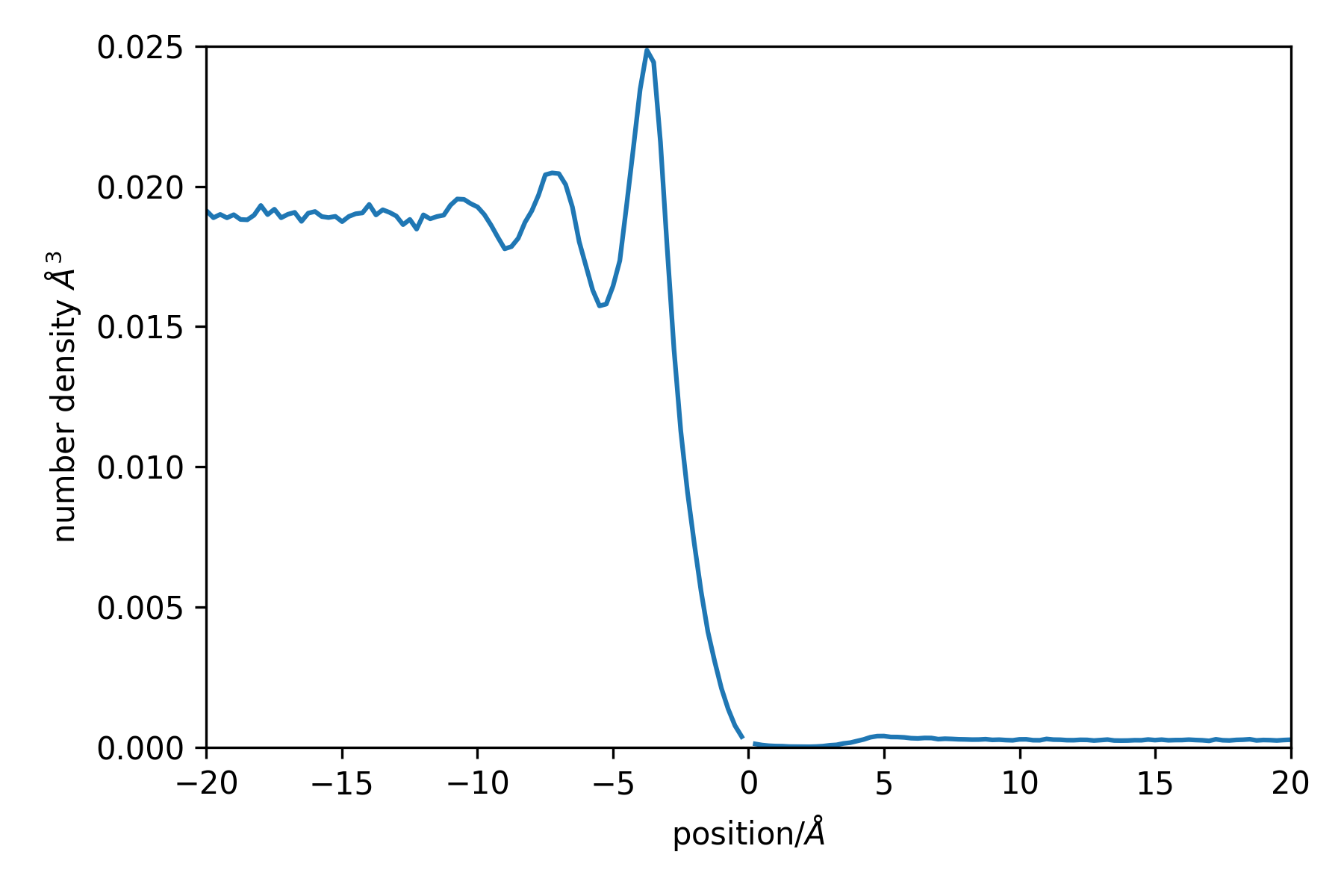
_images/intrinsic_lj.png

Note the missing point at position = 0, this is the delta-function contirbution. Negative positions are within the liquid phase, while positive ones are in the vapour phase.

Time Correlation Functions

class pytim.observables.Correlator(universe=None, observable=None, reference=None)[source]

Computes the (self) correlation of an observable (scalar or vector)

Parameters:

  • observable (Observable) – compute the autocorrelation of this observable. If the observable is None and the reference is not, the survival probability is computed.

  • normalize (bool) – normalize the correlation to 1 at t=0

  • reference (AtomGroup) – if the group passed to the sample() function changes its composition along the trajectory (such as a layer group), a reference group that includes all atoms that could appear in the variable group must be passed, in order to provide a proper normalization. See the example below.

Example:

>>> import pytim
>>> import MDAnalysis as mda
>>> import numpy as np
>>> from pytim.datafiles import WATERSMALL_GRO
>>> from pytim.utilities import lap
>>> #  tmpdir here is specified only for travis
>>> WATERSMALL_TRR = pytim.datafiles.pytim_data.fetch('WATERSMALL_LONG_TRR',tmpdir='./') 
checking presence of a cached copy...

>>> u = mda.Universe(WATERSMALL_GRO,WATERSMALL_TRR)
>>> g = u.select_atoms('name OW')

>>> velocity = pytim.observables.Velocity()
>>> corr = pytim.observables.Correlator(observable=velocity)
>>> for t in u.trajectory[1:]:
...     corr.sample(g)
>>> vacf = corr.correlation()

This produces the following (steps of 1 fs):

(Source code, png, hires.png, pdf)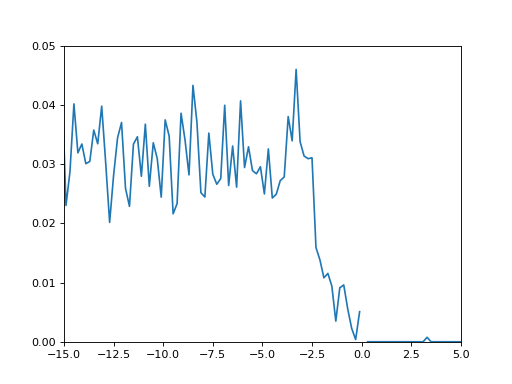

_images/observables-2.png

In order to compute the correlation for variable groups, one should proceed as follows:

>>> corr = pytim.observables.Correlator(observable=velocity,reference=g)
>>> # notice the molecular=False switch, in order for the
>>> # layer group to be made of oxygen atoms only and match
>>> # the reference group
>>> inter = pytim.ITIM(u,group=g,alpha=2.0,molecular=False)
>>> # example only: sample longer for smooth results
>>> for t in u.trajectory[1:10]:
...     corr.sample(inter.atoms)
>>> layer_vacf = corr.correlation()

In order to compute the survival probability of some atoms in a layer, it is possible to pass observable=None together with the reference group:

>>> corr = pytim.observables.Correlator(observable=None, reference = g)
>>> inter = pytim.ITIM(u,group=g,alpha=2.0, molecular=False)
>>>  # example only: sample longer for smooth results
>>> for t in u.trajectory[1:10]:
...     corr.sample(inter.atoms)
>>> survival = corr.correlation()
sample(group)[source]

Sample the timeseries for the autocorrelation function

Parameters:

group (AtomGroup) – compute the observable using this group

correlation(normalized=True, continuous=True)[source]

Calculate the autocorrelation from the sampled data

Parameters:

  • normalized (bool) – normalize the correlation function to: its zero-time value for regular correlations; to the average of the characteristic function for the survival probability.

  • continuous (bool) – applies only when a reference group has been specified: if True (default) the contribution of a particle at time lag \tau=t_1-t_0 is considered only if the particle did not leave the reference group between t_0 and t_1. If False, the intermittent correlation is calculated, and the above restriction is released.

Example:

>>> # We build a fake trajectory to test the various options:
>>> import MDAnalysis as mda
>>> import pytim
>>> import numpy as np
>>> from pytim.datafiles import WATER_GRO
>>> from pytim.observables import Correlator, Velocity
>>> np.set_printoptions(suppress=True,precision=3)
>>>
>>> u = mda.Universe(WATER_GRO)
>>> g = u.atoms[0:2]
>>> g.velocities*=0.0
>>> g.velocities+=1.0
>>>
>>> # velocity autocorrelation along x, variable group
>>> vv = Correlator(observable=Velocity('x'), reference=g)
>>> nn = Correlator(reference=g) # survival probability in group g
>>>
>>> for c in [vv,nn]:
...     c.sample(g)     # t=0
...     c.sample(g)     # t=1
...     c.sample(g[:1]) # t=2, exclude the second particle
...     g.velocities /= 2. # from now on v=0.5
...     c.sample(g)     # t=3
>>>

The timeseries sampled can be accessed using:

>>> print(vv.timeseries) # rows refer to time, columns to particle
[[1.0, 1.0], [1.0, 1.0], [1.0, 0.0], [0.5, 0.5]]
>>>
>>> print(nn.timeseries)
[[True, True], [True, True], [True, False], [True, True]]
>>>

Note that the average of the characteristic function h(t) is done over all trajectories, including those that start with h=0. The correlation \langle h(t)h(0) \rangle is divided by the average \langle h \rangle computed over all trajectores that extend up to a time lag t. The normalize switch has no effect.

>>> # normalized, continuous
>>> corr = nn.correlation()
>>> print (np.allclose(corr, [ 7./7, 4./5, 2./4, 1./2]))
True
>>> # normalized, intermittent
>>> corr = nn.correlation(continuous=False)
>>> print (np.allclose(corr, [ 7./7, 4./5, 3./4, 2./2 ]))
True

The autocorrelation functions are calculated by taking into account in the average only those trajectory that start with h=1 (i.e., which start within the reference group). The normalization is done by dividing the correlation at time lag t by its value at time lag 0 computed over all trajectories that extend up to time lag t and do not start with h=0.

>>> # not normalizd, intermittent
>>> corr = vv.correlation(normalized=False,continuous=False)
>>> c0 = (1+1+1+0.25+1+1+0.25)/7
>>> c1 = (1+1+0.5+1)/5 ; c2 = (1+0.5+0.5)/4 ; c3 = (0.5+0.5)/2
>>> print (np.allclose(corr, [ c0, c1, c2, c3]))
True
>>> # check normalization
>>> np.all(vv.correlation(continuous=False) == corr/corr[0])
True
>>> # not normalizd, continuous
>>> corr = vv.correlation(normalized=False,continuous=True)
>>> c0 = (1+1+1+0.25+1+1+0.25)/7
>>> c1 = (1+1+0.5+1)/5 ; c2 = (1+0.5)/4 ; c3 = (0.5+0.)/2
>>> print (np.allclose(corr, [ c0, c1, c2, c3]))
True
>>> # check normalization
>>> np.all(vv.correlation(continuous=True) == corr/corr[0])
True

Contact Angles

class pytim.observables.ContactAngle(inter, substrate, periodic=None, hcut=0.0, hcut_upper=None, contact_cut=0.0, bins=100, removeCOM=None, store=False)[source]

ContactAngle class implementation that uses interfacial atoms to compute droplet profiles and contact angles using different approaches.

Parameters:

  • interface (PYTIM) – Compute the contact angle for this interface

  • droplet (AtomGroup) – Atom group representative of the droplet

  • substrate (AtomGroup) – Atom group representative of the substrate

  • periodic (int) – direction along which the system is periodic. Default: None, not periodic If None, the code performs best fit to ellipsoids, otherwise, to ellipses If not None, selects the direction of the axis of macroscopic translational invariance: 0:x, 1:y, 2:z

  • hcut (float) – don’t consider contributions from atoms closer than this to the substrate (used to disregard the microscopic contact angle)

  • hcut_upper (float) – don’t consider contributions from atoms above this distance from the substrate default: None

  • bins (int) – bins used for sampling the profile

  • removeCOM (int or array_like) – remove the COM motion along this direction(s). Default: None, does not remove COM motion

Example:

>>> import MDAnalysis as mda
>>> import numpy as np
>>> import pytim
>>> from pytim import observables
>>> from pytim.datafiles import *
>>> 
>>> u = mda.Universe(WATER_DROPLET_CYLINDRICAL_GRO,WATER_DROPLET_CYLINDRICAL_XTC)
>>> droplet = u.select_atoms("name OW")
>>> substrate = u.select_atoms("name C")
>>> inter = pytim.GITIM(universe=u,group=droplet, molecular=False,alpha=2.5,cluster_cut=3.4, biggest_cluster_only=True)
>>> 
>>> # Contact angle calculation using interfacial atoms, angular bining for a cylindrical droplet
>>> # with periodicity along the y (1) axis
>>> 
>>> CA = observables.ContactAngle(inter, substrate, periodic=1,bins=397,removeCOM=0,hcut=5)
>>> for ts in u.trajectory[::]:
...     CA.sample()
>>> # Instantaneous contact angle (last frame) by fitting a circle...
>>> np.round(CA.contact_angle,2)
90.58

>>> 
>>> # ... and using an elliptical fit:
>>> left, right = CA.contact_angles
>>> # left angle
>>> np.round(np.abs(left),2)
79.95

>>> # right angle
>>> np.round(right,2)
83.84

>>> # Contact angles from the averaged binned statistics of
>>> # surface atoms' radial distance as a function of the azimuthal angle
>>> list(np.round(CA.mean_contact_angles,2))
[96.2, 100.68]
property contact_angle

The contact angle from the best-fititng circumference or sphere computed using the current frame

property mean_contact_angle

The contact angle from the best-fititng circumference computed using the location of the interface averaged over the sampled frames

property contact_angles

The contact angles from the best-fititng ellipse or ellipsoid computed using the current frame

property mean_contact_angles

The contact angles from the best-fititng ellipse or ellipsoid computed using the location of the interface averaged over the sampled frames

sample()[source]

samples the profile of a droplet, stores the current atomic coordinates of the liquid surface not in contact with the substrate in the reference frame of the droplet, and optionally the coordinates along the whole trajectory.

static rmsd_ellipsoid(p, x, N, check_coeffs=True)[source]

RMSD between the points x and the ellipsoid defined by the general parameters p of the associated polynomial.

Parameters:

  • p (list) – general coefficients [a,b,c,f,g,h,p,q,r,d]

  • x (ndarray) – points coordinates as a (x,3)-ndarray

  • N (int) – number of points on the ellipsoid that are generated and used to compute the rmsd

  • check_coeffs (bool) – if true, perform additional checks

static ellipse(parmsc, npts=100, tmin=0.0, tmax=6.283185307179586)[source]

Return npts points on the ellipse described by the canonical parameters x0, y0, ap, bp, e, phi for values of the paramter between tmin and tmax.

Parameters:

  • parmsc (dict) – dictionary with keys: x0,y0,a,b,phi

  • tmin (float) – minimum value of the parameter

  • tmax (float) – maximum value of the parameter

  • npts (int) – number of points to use

Returns:

Tuple:

(x,y): coordinates as numpy arrays

static circle(parmsc, npts=100, tmin=0.0, tmax=6.283185307179586)[source]

Return npts points on the circle described by the canonical parameters R, x0, y0 for values of the paramter between tmin and tmax.

Parameters:

  • parmsc (dict) – dictionary with keys: R, x0, y0

  • tmin (float) – minimum value of the parameter

  • tmax (float) – maximum value of the parameter

  • npts (int) – number of points to use

Returns:

Tuple:

(x,y): coordinates as numpy arrays

static ellipsoid(parmsc, npts=1000)[source]

Compute npts points on the ellipsoid described by the affine parameters T, v

Parameters:

  • parmsc (dict) – dictionary with keys: T (3x3 matrix), v (3x1 vector)

  • npts (int) – number of points to use

Returns:

Tuple:

(x,y,z) : coordinates of points on the ellipsoid as ndarrays

sample_theta_R(theta, r, h)[source]

given a set of angles (theta), radii (r) and elevations (h), compute the mean profile h(r) by taking the binned average values of h and r.

fit_circle(use='frame', nonlinear=True, bins=1)[source]

fit an arc through the profile h(r) sampled by the class

Parameters:

  • use (str) – ‘frame’ : use the positions of the current frame only (default) ‘histogram’: use the binned values sampled so far ‘stored’ : use the stored surface atoms positions, if the option store=True was passed at initialization

  • bins (int) – the number of bins to use along the symmetry direction (cylinder axis, azimuthal angle)

Returns:

a list including, for each of the bins:

tuple:

radius, base radius, cos(theta), center

fit_ellipse(use='frame', nonlinear=True, bins=1)[source]

fit an ellipse through the points sampled by the class. See implementation details in _fit_ellipsoid()

Parameters:

  • use (str) – ‘frame’ : use the positions of the current frame only (default) ‘histogram’: use the binned values sampled so far ‘stored’ : use the stored surface atoms positions, if the option store=True was passed at initialization

  • bins (int) – the number of bins to use along the symmetry direction (cylinder axis, azimuthal angle)

Returns:

a list including, for each of the bins, a tuple with elements:

list:

parms: parameters of the ellipse polynomial in general form: a[0] x^2 + a[1] x y + a[2] y^2 + a[3] x + a[4] y = 0

dict:

parmsc: dictionary of parameters in canoncial form: (a,b, x0,y0,phi, e) with a,b the major and minor semiaxes, x0,y0 the center, phi the angle (in rad) between x axis and major axis, and e the eccentricity.

list:

theta: [left contact angle, right contact angle]

fit_ellipsoid(use='frame', nonlinear=True, bins=1)[source]

fit an ellipsoid through the points sampled by the class. See implementation details in _fit_ellipsoid()

:param str use : ‘frame’ : use the positions of the current frame only (default) ‘histogram’: use the binned values sampled so far ‘stored’ : use the stored surface atoms positions, if the option store=True was passed at initialization :param int bins : the number of bins to use along the symmetry direction (cylinder axis, azimuthal angle)

Returns:

a list with a tuple (parms,parmsc,theta, rmsd) for each of the bins; If only one bin is present, return just the tuple.

array:

parms : array of parameters of the ellipsoid equation in general form: a[0] x^2 + a[1] y^2 + a[2] z^2 + a[3] yz + a[4] xz + a[5] xy + a[6] x + a[7] y + a[8] z + a[9] = 0, otherwise.

dict:

parmsc : dictionary with parameters of the ellipsoid affine form (T,v), such that the ellipsoid points are r = T s + v, if s are points from the unit sphere centered in the origin.

float:

theta : the contact angle as a function of the azimuthal angle phi from phi=0, aligned with (-1,0,0) to 2 pi.

float:

rmsd : the rmsd to the best fit (linear or nonlinear) ellipsoid

3D Distributions

class pytim.observables.DistributionFunction(universe, order, nbins=75, start=None, stop=None, step=None, generalized_coordinate=None, generalized_coordinate2=None, observable=None, observable2=None, max_distance=None, coords_in=['x', 'y', 'z'], coords_out=['x', 'y', 'z'], kargs1=None, kargs2=None)[source]

Calculates a 3d distribution function of some observable from two groups.

The two functions must return an array (of scalars or of vectors) having the same size of the group. The scalar product between the two functions is used to weight the distriution function.

sdf(x,y,z) = \frac{1}{N}\left\langle \sum_{i\neq j} \delta(x-x_i,y-y_i,z-z_i)\ f_1(r_i,v_i)\cdot f_2(r_j,v_j) \right\rangle

Parameters:

  • max_distance (double) – compute the sdf up to this distance along the axes. If a list or an array is supplied, each element will determine the maximum distance along each axis. If ‘full’ is supplied (default) computes it up to half of the smallest box side.

  • nbins (int) – number of bins used for the sampling in all directions. Supply a list or an array to use a different number of bins along each of the directions

  • observable (Observable) – observable for the first group

  • observable2 (Observable) – observable for the second group

Example:

>>> import MDAnalysis as mda
>>> import numpy as np
>>> import pytim
>>> from pytim import observables
>>> from pytim.datafiles import *
>>>
>>> u = mda.Universe(WATER_GRO,WATER_XTC)
>>> oxygens = u.select_atoms("name OW")
>>>
>>> nres = observables.NumberOfResidues()
>>>
>>> rdf = observables.RDF(u,nbins=120,observable=nres,observable2=nres)
>>>
>>> interface = pytim.ITIM(u,alpha=2.,group=oxygens,cluster_cut=3.5,molecular=False)
>>>
>>> for ts in u.trajectory[::50]:
...     layer=interface.layers[0,0]
...     rdf.sample(layer,layer)
>>> rdf.count[0]=0
>>> np.savetxt('RDF3D.dat', np.column_stack((rdf.bins,rdf.rdf)))

Note that one needs to specify neither both groups, not both observables. If only the first group (observable) is specified, the second is assumed to be the same as the first, as in the following example:

>>> rdf1 = observables.RDF(u,observable=nres)
>>> rdf2 = observables.RDF(u,observable=nres)
>>> rdf3 = observables.RDF(u,observable=nres,observable2=nres)
>>>
>>> rdf1.sample(layer)
>>> rdf2.sample(layer,layer)
>>> rdf3.sample(layer,layer)
>>> print (np.all(rdf1.rdf[:]==rdf2.rdf[:]))
True
>>> print (np.all(rdf1.rdf[:]==rdf3.rdf[:]))
True

Free Volume

class pytim.observables.FreeVolume(universe, npoints=None)[source]

Calculates the fraction of free volume in the system, or its profile.

Note that this does not fit in the usual observable class as it can not be expressed as a property of particles, and needs some kind of gridding to be calculated.

Parameters:

  • universe (Universe) – the universe

  • npoints (int) – number of Monte Carlo sampling points (default: 10x the number of atoms in the universe)

Returns:

Tuple:

free volume, error : A tuple with the free volume and the estimated error

Examples:

>>> import MDAnalysis as mda
>>> import numpy as np
>>> import pytim
>>> from pytim.datafiles import CCL4_WATER_GRO, _TEST_BCC_GRO
>>> 
>>> u = mda.Universe(CCL4_WATER_GRO)
>>> inter = pytim.ITIM(u) # just to make sure all radii are set
>>> np.random.seed(1) # ensure reproducibility of test
>>> FV = pytim.observables.FreeVolume(u)
>>> bins, prof ,err = FV.compute_profile()
>>> 
>>> free, err = FV.compute()
>>> print ('{:0.3f} +/- {:0.3f}'.format(free,err))
0.431 +/- 0.001

>>> # strict test on bcc volume fraction
>>> u = mda.Universe(_TEST_BCC_GRO)
>>> # we add some random gitter to avoid singular matrices
>>> u.atoms.positions += np.random.random(u.atoms.positions.shape)*1e-5
>>> inter = pytim.GITIM(u,radii_dict={'C':10.*np.sqrt(3.)/4.})
>>> nsamples = int(1e5)
>>> FV = pytim.observables.FreeVolume(u,npoints = nsamples)
>>> np.random.seed(1) # ensure reproducibility of test
>>> free, err = FV.compute()
>>> np.isclose(free,1.0-0.6802,rtol=1e-3)
True
>>> np.random.seed(1) # ensure reproducibility of test
>>> lst, _ = FV._compute()
>>> np.isclose(free,1.0-len(lst)*1.0/nsamples, rtol=1e-6)
True
compute_profile(inp=None, nbins=30, direction=2)[source]

Compute a profile of the free volume fraction

Parameters:

  • inp (AtomGroup) – compute the volume fraction of this group, None selects the complete universe

  • nbins (int) – number of bins, by default 30

  • direction (int) – direction along wich to compute the the profile, z (2) by default

Returns:

Tuple:

bins,fraction,error: the left limit of the bins, the free volume fraction in each bin, the associated std deviation

compute(inp=None)[source]

Compute the total free volume fraction in the simulation box

Parameters:

  • inp (AtomGroup) – compute the volume fraction of this group, None selects the complete universe

  • nbins (int) – number of bins, by default 30

Returns:

Tuple:

fraction, error: the free volume fraction and associated error

Local Reference Frame

Misc

class pytim.observables.IntrinsicDistance(interface, symmetry='default', mode='default')[source]

Initialize the intrinsic distance calculation.

Parameters:

  • interface (PYTIM) – compute the intrinsic distance with respect to this interface

  • symmetry (str) – force calculation using this symmetry, if availabe (e.g. ‘generic’, ‘planar’, ‘spherical’) If ‘default’, uses the symmetry selected in the PYTIM interface instance.

Example:

>>> import MDAnalysis as mda
>>> import pytim
>>> import numpy as np
>>> from pytim import observables
>>> from pytim.datafiles import MICELLE_PDB
>>> u = mda.Universe(MICELLE_PDB)
>>> micelle = u.select_atoms('resname DPC')
>>> waterox = u.select_atoms('type O and resname SOL')
>>> inter = pytim.GITIM(u,group=micelle, molecular=False, alpha=2.0)
>>> dist  = observables.IntrinsicDistance(interface=inter)
>>> d = dist.compute(waterox)
>>> np.set_printoptions(precision=3,threshold=10)
>>> print(d)
[25.733  8.579  8.852 ... 18.566 13.709  9.876]

>>> np.set_printoptions(precision=None,threshold=None)
compute(inp, kargs=None)[source]

Compute the intrinsic distance of a set of points from the first layers.

Parameters:

positions (ndarray) – compute the intrinsic distance for this set of points

class pytim.observables.LayerTriangulation(interface, return_triangulation=True, return_statistics=True)[source]

Computes the triangulation of the surface and some associated quantities. Notice that this forces the interface to be centered in the box.

Parameters:

  • universe (Universe) – the MDAnalysis universe

  • interface (ITIM) – compute the triangulation with respect to it

  • layer (int) – (default: 1) compute the triangulation with respect to this layer of the interface

  • return_triangulation (bool) – (default: True) return the Delaunay triangulation used for the interpolation

  • return_statistics (bool) – (default: True) return the Delaunay triangulation used for the interpolation

Returns:

Observable LayerTriangulation

Example:

>>> import pytim
>>> import MDAnalysis as mda
>>> from pytim.datafiles import WATER_GRO

>>> interface = pytim.ITIM(mda.Universe(WATER_GRO),molecular=False)
>>> surface   = pytim.observables.LayerTriangulation(                            interface,return_triangulation=False)
>>> stats     = surface.compute()
>>> print ("Surface= {:04.0f} A^2".format(stats[0]))
Surface= 6328 A^2
class pytim.observables.LocalReferenceFrame(*arg, **kwarg)[source]

Compute the local surface using a definition based on that of S. O. Yesylevskyy and C. Ramsey, Phys.Chem.Chem.Phys., 2014, 16, 17052 modified to include a guess for the surface normal direction

Example (note that this example started failing on the last output line with opposite signs for x and y. Could be an instability of the SVD, thus the test is removed from the docstring):

>>> import MDAnalysis as mda
>>> import pytim
>>> from pytim.datafiles import WATER_GRO
>>> import numpy as np
>>> g=mda.Universe(WATER_GRO).select_atoms('name OW')
>>> inter = pytim.ITIM(g,molecular=False)
>>> frame = pytim.observables.LocalReferenceFrame().compute(g)
>>> np.set_printoptions(precision=6,threshold=2,suppress=None)
>>> print(frame) 
[[[-0.330383  0.740913 -0.584718]
  [-0.937619 -0.328689  0.113291]
  [ 0.108252 -0.585672 -0.803287]]

 [[-0.98614   0.164904  0.018286]
  [-0.146148 -0.811192 -0.566223]
  [ 0.078538  0.561048 -0.824049]]

 [[-0.921816 -0.28798  -0.259465]
  [ 0.182384 -0.912875  0.365233]
  [ 0.342039 -0.289355 -0.894026]]

 ...

 [[-0.740137 -0.557695  0.375731]
  [ 0.369404  0.129692  0.920174]
  [-0.561906  0.819852  0.110024]]

 [[-0.198256 -0.724093  0.660594]
  [ 0.64637  -0.603238 -0.467236]
  [-0.736818 -0.334356 -0.587627]]

 [[ 0.268257 -0.337893 -0.902146]
  [ 0.233933 -0.885591  0.401253]
  [-0.934513 -0.31868  -0.158522]]]

>>> np.set_printoptions()
compute(inp, kargs=None)[source]

Compute the local reference frame

Parameters:

inp (AtomGroup) – the group of atoms that define the surface

Returns:

a (len(inp),3,3) set of coordinates defining the local axes, with the slice [:2:] defining the normal vectors

Basic Observables

class pytim.observables.Charge(*arg, **kwarg)[source]

Atomic charges

compute(inp, kargs=None)[source]

Compute the observable.

Parameters:

inp (AtomGroup) – the input atom group

Returns:

an array of charges for each atom in the group

class pytim.observables.Force(arg='xyz', **kwarg)[source]

Atomic forces

compute(inp, kargs=None)[source]

Compute the observable.

Parameters:

inp (AtomGroup) – the input atom group

Returns:

atomic forces

class pytim.observables.Mass(*arg, **kwarg)[source]

Atomic masses

compute(inp, kargs=None)[source]

Compute the observable.

Parameters:

inp (AtomGroup) – the input atom group

Returns:

an array of masses for each atom in the group

class pytim.observables.Number(*arg, **kwarg)[source]

The number of atoms.

compute(inp, kargs=None)[source]

Compute the observable.

Parameters:

inp (AtomGroup) – the input atom group

Returns:

one, for each atom in the group

class pytim.observables.NumberOfResidues(*arg, **karg)[source]

The number of residues.

Instead of associating 1 to the center of mass of the residue, we associate 1/(number of atoms in residue) to each atom. In an homogeneous system, these two definitions are (on average) equivalent. If the system is not homogeneous, this is not true anymore.

compute(inp, kargs=None)[source]

Compute the observable.

Parameters:

inp (AtomGroup) – the input atom group

Returns:

one, for each residue in the group

class pytim.observables.Orientation(universe, options='')[source]

Orientation of a group of points.

Parameters:

options (str) – optional string. If normal is passed, the orientation of the normal vectors is computed If the option ‘molecular’ is passed at initialization the coordinates of the second and third atoms are folded around those of the first.

compute(inp, kargs=None)[source]

Compute the observable.

Parameters:

inp (ndarray) – the input atom group. The length must be a multiple of three

Returns:

the orientation vectors

For each triplet of positions A1,A2,A3, computes the unit vector between A2-A1 and A3-A1 or, if the option ‘normal’ is passed at initialization, the unit vector normal to the plane spanned by the three vectors.

class pytim.observables.Position(arg='xyz', **kwarg)[source]

Atomic positions

Example: compute the projection on the xz plane of the first water molecule

>>> import MDAnalysis as mda
>>> import pytim
>>> u = mda.Universe(pytim.datafiles.WATER_GRO)
>>> proj = pytim.observables.Position('xz')
>>> with np.printoptions(precision=3):
...     print(proj.compute(u.residues[0].atoms) )
[[28.62 11.37]
 [28.42 10.51]
 [29.61 11.51]]
compute(inp, **kwarg)[source]

Compute the observable.

Parameters:

inp (AtomGroup) – the input atom group

Returns:

atomic positions

class pytim.observables.Velocity(arg='xyz', **kwarg)[source]

Atomic velocities

compute(inp, kargs=None)[source]

Compute the observable.

Parameters:

inp (AtomGroup) – the input atom group

Returns:

atomic velocities